MÉTODOS DE SOLUCIÓN DE UN SISTEMA DE ECUACIONES LINEALES Y TIPOS DE SOLUCIÓN

Métodos de solución de sistemas de ecuaciones lineales:
Gauss.
Gauss Jordán.
Determinantes o Regla de Cramer.
Adjunta de una matriz.
Sustitución.
Solución De Sistemas De Ecuaciones Por El Método de Gauss:

Este método se basa en la idea de reducir la matriz aumentada a una forma que sea lo suficientemente sencilla como para poder resolver el sistema de ecuaciones a simple vista.

Matriz Triangular Inferior (Matriz aumentada)

En la última etapa del ejemplo anterior se obtuvo la matriz aumentada. Después de la cual, fue fácil obtener la solución
X = -23.8, Y = 32.6, Z = -7.8 para el sistema original de ecuaciones. El sistema de ecuaciones correspondientes es:
 X + 2Y + 3Z = 18                       Y + 2Z = 17                    Z = -7.8

 Sustituimos las ecuaciones y la solución  Z = -7.8, Y = 32.6, X = -23.8 se hace obvia examinando la raíz aumentada.


Solución De Sistemas De Ecuaciones Por El Método De Gauss-Jordán:

 Se definió un poco la forma de solución de  un sistema de ecuaciones lineales una vez que su matriz aumentada tiene la forma escalonada reducida. Ahora se dará un procedimiento esquemático, conocido como eliminación de Gauss-Jordán, que puede ser empleado para llevar cualquier matriz a la forma escalonada reducida.

Matriz Identidad


El sistema de ecuaciones correspondientes es:

 X = -23.8                       Y = 32.6                    Z = -7.8



Solución De Sistemas De Ecuaciones Por El Método de determinantes o regla de cramer:

Los pasos a seguir para calcular los sistemas de ecuaciones según la regla de Cramer son los          

                4. Calculamos X, Y y Z
X = |Δ1|/|A| = -238/10 = -23.8
Y = |Δ2|/|A| = 326/10 = 32.6
Z = |Δ3|/|A| = -78/10 = -7.8

Solución De Sistemas De Ecuaciones Por El Metodo De La Inversa

Sabiendo calcular la matriz inversa y multiplicando matrices también es posible resolver un sistema de ecuaciones lineales, siempre y cuando éste sea de Crámer (es decir, tenga igual número de ecuaciones que de incógnitas y el determinante de la matriz de coeficientes no sea nulo).
 
Los pasos a seguir para calcular los sistemas de ecuaciones utilizando la inversa son los siguientes:
                1. Calcular la inversa de la matriz A:


                2.- Multiplicar la inversa de la matriz A por la matriz B

X = 18(-31/10) + 20(17/10) + 10(-1/5) = -23.8
Y = 18(37/10) + 20(-19/10) + 10(2/5) = 32.6
Z = 18(-11/10) + 20(7/10) + 10(-1/5) = -7.8



Método por sustitución:

El método de sustitución consiste en despejar en una de las ecuaciones cualquier incógnita, preferiblemente la que tenga menor coeficiente, para, a continuación, sustituirla en otra ecuación por su valor.


En la primera ecuación, seleccionamos la incógnita ´y´ por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.

El siguiente paso será sustituir cada ocurrencia de la incógnita ´y´ en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  ´x´.


Al resolver la ecuación obtenemos el resultado x=5, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos y=7, con lo que el sistema queda ya resuelto.


Matriz Inversa:

Una matriz inversa es una matriz que multiplicado por la matriz original obtiene la matriz de identidad. El inverso de un cuadrado  n x n matriz, es otro n x n matriz denotado por A-1  :


Donde es la n x n matriz identidad. Es decir, multiplicando su inversa una matriz produce una matriz de identidad. No todas las matrices tiene una matriz inversa. Si el determinante de la matriz es cero, entonces no tendrá una inversa y la matriz se dice que es singular. Sólo no singular matrices tienen inversas.

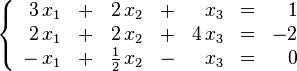
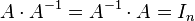INTERPRETACIÓN GEOMÉTRICA DE LAS SOLUCIONES

Cada ecuación representa un plano en el espacio tridimensional. Luego se trata de estudiar la posición relativa de tres planos en el espacio. Las soluciones del sistema son geométricamente los puntos de intersección de los tres planos, los casos son:

=Un punto único. Sistema compatible determinado.. Los tres planos se cortan en P.

=Una recta. Son soluciones todos los puntos representativos de la recta común. Sistema compatible indeterminado con un grado de libertad. Los planos se cortan en r.

=Un plano. Los planos son coincidentes. El sistema es compatible indeterminado con dos grados de libertad.

=Ningún punto. El sistema es incompatible. Esta situación se presenta geométricamente de distintas maneras. Para estudiar las posiciones relativas de los planos hay que tomarlos de dos en dos.

=Se pueden presentar varios casos: Que los planos sean paralelos:

CLASIFICACIÓN DE LOS SISTEMAS DE ECUACIONES LINEALES Y TIPOS DE SOLUCIÓN

Podemos clasificar los sistemas de ecuaciones lineales según su número de soluciones de la siguiente forma:
Sistemas con una solución: Las ecuaciones del sistema son rectas secantes.
Se cortan en un punto (x, y) que es la solución del sistema
Sistemas sin solución: Las ecuaciones del sistema son rectas paralelas. No tienen ningún punto en común, y por tanto no hay solución
Sistemas con infinitas soluciones: Las ecuaciones del sistema son rectas coincidentes. Tienen todos los puntos en común, y por tanto todos ellos son solución

=Tipos de Solución=
=Sustitución=
El método de sustitución consiste en despejar en una de las ecuaciones cualquier incógnita, preferiblemente la que tenga menor coeficiente, para, a continuación, sustituirla en otra ecuación por su valor.

=Igualación=
El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones.

=Reducción=
Este método suele emplearse mayoritariamente en los sistemas lineales, siendo pocos los casos en que se utiliza para resolver sistemas no lineales. El procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste en transformar una de las ecuaciones (generalmente, mediante productos), de manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con el mismo coeficiente y distinto signo. A continuación, se suman ambas ecuaciones produciéndose así la reducción o cancelación de dicha incógnita, obteniendo así una ecuación con una sola incógnita, donde el método de resolución es simple. Por ejemplo, en el sistema:

DEFINICIÓN DE SISTEMAS DE ECUACIONES LINEALES

En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:

   

2.5 Calculo de la inversa de una matriz.

En matemáticas, en particular en álgebra lineal, una matriz cuadrada A de orden n se dice que es invertible, no singular, no degenerada o regular si existe otra matriz cuadrada de orden n, llamada matriz inversa de A y representada como A⁻¹, tal que:

,

donde I_n es la matriz identidad de orden n y el producto utilizado es el producto de matrices usual.

Una matriz no invertible se dice que es singular o degenerada. Una matriz es singular si y solo si su determinante es nulo.

2.4 Transformaciones elementales por región. Escalonamiento de una matriz. Rango de una matriz.

Transformaciones elementales en las filas, Las fases de una matriz, Rango de una matriz

Si se intercambian dos filas cualesquiera de una matriz dada, llamamos a esta operación una operación de transformación elemental en las filas de una matriz. Se denota por R¬ij¬¬, lo cual implica que se intercambian las filas i y j de la matriz dada. Esta operación también se denota por R¬i¬ <→ R-j¬.

Un punto digno de notar es que esta operación no es de naturaleza singular. De hecho se ha demostrado, que todas las matrices no singulares son el resultado de la transformación elemental en la fila de una matriz . Si esto es cierto, entonces podemos concluir, que para todas las matrices no singulares también tenemos una matriz inversa, la cual tampoco es singular y es también el resultado de la transformación elemental en la fila de una matriz. Esta matriz elemental se denomina la matriz identidad I y tenemos el resultado A x I = A-1

En álgebra lineal, el rango de una matriz es el número máximo de columnas (filas respectivamente) que son linealmente independientes. El rango fila y el rango columna siempre son iguales: este número es llamado simplemente rango de A (prueba más abajo). Comúnmente se expresa como rg(A).

El número de columnas independientes de una matriz A de m filas y n columnas es igual a la dimensión del espacio columna de A. También la dimensión del espacio fila determina el rango. El rango de A será, por tanto, un número no negativo, menor o igual que el mínimo entre m y n:

2.3 Clasificación de las matrices.

Diferentes tipos de matriz

1). Matriz columna: Una matriz con n filas y 1 columna, se denomina matriz columna. Esta matriz es de tipo m x 1.

Por ejemplo: 

2). Matriz fila: Una matriz que tiene una fila y n columnas, se dice que es una matriz fila. Esta matriz es del tipo 1 x n.

Por ejemplo: 

3). Matriz Cuadrada: Una matriz en la cual el número de columnas es igual al número de filas, se conoce como una matriz cuadrada. Una matriz de orden n es aquella que tiene n filas y n columnas. La propiedad aceptada en la matriz cuadrada es que dos o más matrices cuadradas de orden idéntico, pueden multiplicarse, sumarse y restarse.

Por ejemplo: 

4). Matriz diagonal: En una matriz cuadrada, los elementos para los cuales i = j, se denominan elementos diagonales. Una matriz cuadrada donde cada elemento, excepto los elementos diagonales, son iguales a cero, es llamada matriz diagonal. La matriz diagonal se denomina a veces matriz diagonal rectangular.

Por ejemplo: 

5). Matriz identidad o unidad: Se dice que una matriz es la matriz identidad o unidad, si cada elemento de la diagonal principal de la matriz particular es 1. La matriz identidad generalmente es denotada por ‘I’. Este tipo de matriz tiene la siguiente propiedad:

AI = A y IA = A

Por ejemplo: 

6). Matriz cero o nula: Se trata de una matriz en la cual cada elemento es igual a 0. Se representa como ‘0’. Si ‘O’ es la matriz cero m × n y A es cualquier matriz m × n, entonces A + O = O A. En consecuencia O es la identidad aditiva de la suma de matrices.

Por ejemplo: 

7). Matriz simétrica: Una matriz simétrica se refiere a la matriz cuadrada cuyo valor es igual al transpuesto de la matriz. Es decir, .La simetría de la diagonal simétrica está relacionada con la diagonal principal. Por otra parte, toda matriz diagonal es simétrica.

Por ejemplo: 

8). Matriz asimétrica: La matriz asimétrica también es conocida como matriz antimétrica o antisimétrica. Se trata de una matriz cuyo valor de transposición es negativo de su valor. Es decir,

A = -AT.

-
Bibliografia:
 http://mitecnologico.com/igestion/Main/ClasificacionDeLasMatrices#sthash.vBxaEE8F.dpuf

2.2 Operaciones con matrices.

La matriz suma se obtienen sumando los elementos de las dos matrices que ocupan la misma misma posición; Para realizar la resta lo único que varia es el signo.

A continuación se muestran algunos ejemplos de operaciones que se realizan y la forma en que se resuelven las matrices.

2.1 Definición de matriz, notación y orden.

una matriz es una tabla cuadrada o rectangular de datos llamados elementos o entradas de la matriz, ordenados en filas y columnas.
Una matriz puede sumarse, multiplicarse y descomponerse varias formas. Comunmente se dice que una matriz m por n tiene un orden ("orden" tiene el significado de tamaño)

En la matriz una fila es cada linea horizontal y una columna es cada una de las lineas verticales.
Casi siempre, se denotan a las letras mayusculas mientras que se utilizan las correspondientes letras en minusculas para denotar a los elementos de las mismas.

Donald en el país de las matemáticas.

Link del video: ¡¡Donald en el país de las matemáticas!!

1.6 Ecuaciones polinomicas

Una raíz del polinomio p es un complejo z tal que p(z)=0.

Un resultado importante de esta definición es que todos los polinomios de grado n tienen exactamente n soluciones en el campo complejo, esto es, tiene exactamente n complejos z que cumplen la igualdad p(z)=0, contados con sus respectivas multiplicidades. 

A esto se lo conoce como Teorema Fundamental del Álgebra, y demuestra que los complejos son un cuerpo algebraicamente cerrado. Por esto los matemáticos consideran a los números complejos unos números más naturales que los números reales a la hora de resolver ecuaciones.

Ya podemos encontrar todas las soluciones de una ecuación como:

zn + 23 = 0 → z = n√-23

Serán n soluciones.

O las soluciones de ecuaciones como:

zn/m +1 = 0 → z = n√(-1)m

Cualquier complejo elevado a m está univaluado, nos proporcionará un único valor.

Si m/n es irreducible, tendremos n soluciones. Si es reducible, m/n = p/q, y tendremos q < n soluciones distintas.Es importante, por tanto, simplificar m/n siempre.

Además supongamos que hemos simplificado hasta alcanzar m/n. Tomemos una solución de las n posibles.

Al elevarla a n/m debería darnos z, pero nos dará m valores y solo uno de ellos es z.

1.5 Teorema de Moivre,potencias y extracciones de raíces de un numero complejo.

La fórmula de De Moivre nombrada así por Abraham de Moivre afirma que para cualquier número complejo (y en particular, para cualquier número real) x y para cualquier entero n se verifica que:

Esta fórmula es importante porque conecta a los números complejos (i significa unidad imaginaria) con la trigonometría. La expresión "cos x + i sen x" a veces se abrevia como cis x.

Al expandir la parte izquierda de la igualdad y comparando la parte real con la imaginaria, es posible derivar expresiones muy útiles para cos(nx) y sen(nx) en términos de cos(x) y sen(x). Además, esta fórmula puede ser utilizada para encontrar expresiones explícitas para la enésima raíz de la unidad, eso es, números complejos z tal que zn = 1.

1.4 Forma polar y exponencial de un numero complejo

Un número complejo en forma polar consta de dos componentes: módulo y argumento.

Módulo de un número complejo

El módulo de un número complejo es el módulo del vector determinado por el origen de coordenadas y su afijo. Se designa por |z|.

           

Argumento de un número complejo

El argumento de un número complejo es el ángulo que forma el vector con el eje real. Se designa por arg(z).

Expresión de un número complejo en forma polar.

z = rα

|z| = r r es el módulo.

arg(z) = a a es el argumento.

1.3 Potencias de "i", modulo o valor absoluto de un numero complejo.

Por un largo tiempo se pensó que la obtención de la raíz cuadrada de un número negativo era imposible. Una teoría general mencionaba que ningún número puede continuar negativo después haberse elevado al cuadrado. Sin embargo, con el descubrimiento de los números complejos, este estudio se detuvo completamente. Ahora es posible obtener la raíz cuadrada de números negativos y, sin embargo esta es seguida de un símbolo ‘i’. Esta “i” representa el término imaginario, porque tal número no existe en la realidad.

El módulo o valor absoluto es un concepto esencial de las matemáticas, ya sea respecto a los números reales o complejos. Ya sabemos que el módulo de un número es siempre el número mismo removiéndole su signo de magnitud. Es decir, si el número es positivo, entonces su módulo nos da, de nuevo el mismo número, pero si el número dado es negativo, entonces su módulo sería, la forma positiva de ese número.

El uso de los números imaginarios puede estar presente en muchos campos, pero principalmente lo podemos encontrar en el teorema fundamental de álgebra para encontrar la raíz cuadrada de números negativos.

http://mitecnologico.com/igestion/Main/ModuloOValorAbsolutoDeUnNumeroComplejo#sthash.nAL1q6YU.dpuf

1.2 Operaciones fundamentales con números complejos.

1.2 Operaciones fundamentales con números complejos.

Existen una gran variedad de operaciones que pueden realizarse con los números complejos. La suma, resta, división y multiplicación constituyen las operaciones básicas que pueden realizarse con los números complejos.

Suma: La operación de sumar dos números complejos x + yi y c + di puede expresarse como:

 (x + yi) + (c + di) = (x + c) + (y + d)i

Esto es, es posible observar que las partes correspondientes de los números reales se suman juntos y que se hace lo mismo con la parte imaginaria.

Examinemos un ejemplo para entender la operación más plenamente:

Imaginemos que debemos expresar (1 + 8i) + (4 + 5i) en forma compleja.

Entonces, sumando la parte real y la parte imaginaria por separado, obtenemos

(1 + 4) + (8 + 5) i

= 5 + 13i

Resta: La operación de restar dos números complejos x + yi y c + di puede expresarse como:

(x + yi) - (c + di) = (x + c) - (y + d)i

Veamos un ejemplo de la resta de dos números complejos:

Imaginemos que debemos expresar (1+ 8i) - (−4 - 5i) en forma compleja.

Entonces, restando la parte real y la parte imaginaria separadamente, obtenemos

= (1 - 4) - (8 - 5)i

= −3 – 3i

Multiplicación: La operación de Multiplicar dos números complejos x + yi e c + di puede expresarse como:

(x + y i) (c + d i) = (x c - y d) + (x + d yc) i

Sin embargo, esta multiplicación puede realizarse aplicando las propiedades básicas de la Multiplicación de los Números Reales, y recordando la regla básica de los números complejos, esto es, i2 = −1.

Veamos un ejemplo:

Imaginemos que debemos expresar (2 + 3i) (2 - 2i), en forma compleja.

Usando la propiedad distributiva, obtenemos

= (2 + 3i) (2 - 2i) = (2 + 3i) 2 + (2 + 3i) (- 2i)

= 4 + 6i – 4i - 6i2

Agrupando los mismos términos y aplicando la propiedad i2 = −1 obtenemos,

= 4 + 6i – 4i + 6

= 10 + 2i

División: La operación de Dividir dos números complejos (8 + 4 i) y (1 - i) puede expresarse como:

(8 + 4 i) / (1 - i)

En primer lugar, multiplicando el numerador y el denominador con el conjugado del denominador de la expresión anterior, obtenemos

[(8 + 4 i) (1 + i)]

Agrupando y multiplicando los términos semejantes,

[(8 + 4 i) (1 + i)] / [(1 - i) (1 + i)] =

[8 + 4 i + 8 i + 4 i 2] / [1 - i + i - i 2]

= (4 + 12 i) / (2)

= 2 + 6 i

1.1 Definición y origen de los números complejos

1.1 Definición y origen de los números complejos

Los números complejos conforman un grupo de cifras resultantes de la suma entre un número real y uno de tipo imaginario. Un número real, de acuerdo a la definición, es aquel que puede ser expresado por un número entero (4, 15, 2686) o decimal (1,25; 38,1236; 29854,152). En cambio, un número imaginario es aquél cuyo cuadrado es negativo. El concepto de número imaginario fue desarrollado por Leonhard Euler en 1777, cuando le otorgó a v-1 el nombre de i (de “imaginario”).

Cabe resaltar que el cuerpo de cada número real está formado por pares ordenados (a, b). El primer componente (a) es la parte real, mientras que el segundo componente (b) es la parte imaginaria. Los números imaginarios puros son aquellos que sólo están formados por la parte imaginaria (por lo tanto, a=0).

Los números complejos componen el denominado cuerpo complejo (C). Cuando el componente real a es identificado con el correspondiente complejo (a, 0), el cuerpo de estos números reales (R) se transforma en un subcuerpo de C. Por otra parte, C conforma un espacio vectorial de dos dimensiones sobre R. Esto demuestra que los números complejos no admiten la posibilidad de mantener un orden, a diferencia de los números reales.

Información obtenida de:Definición de números complejos - Qué es, Significado y Concepto http://definicion.de/numeros-complejos/#ixzz3kLkEf2pO

Breve historia de los números complejos.
 

Fecha aproximada	Persona	Evento
50	Heron de Alejandria	Primero en encontrar raíz cuadrada de un numero negativo
850	Mahavira de India	Decía que un número complejo no tenía raíz cuadrada, ya que no era cuadrado.
1545	Cardano de Italia	Las soluciones de las ecuaciones cubicas implican raíces cuadradas de números negativos.
1637	Descartes de Francia	Introdujo los términos “real” e “imaginario”.
1748	Euler de Suiza	Uso i para raiz de -1
1832	Gauss de Alemania	Introdujo el termino número complejo.

Sub-temas Unidad 1 Números complejos

1.1 Definición y origen de los números complejos.
1.2 Operaciones fundamentales con números complejos.
1.3 Potencias de i, modulo o valor absoluto de un numero complejo.
1.4 Forma polar y exponencial de un numero complejo.
1.5 Teorema de Moivre, potencias y extracciones de raíces de un numero complejo.
1.6 Ecuaciones polinomicas.