2.5 Calculo de la inversa de una matriz.

En matemáticas, en particular en álgebra lineal, una matriz cuadrada A de orden n se dice que es invertible, no singular, no degenerada o regular si existe otra matriz cuadrada de orden n, llamada matriz inversa de A y representada como A⁻¹, tal que:

,

donde I_n es la matriz identidad de orden n y el producto utilizado es el producto de matrices usual.

Una matriz no invertible se dice que es singular o degenerada. Una matriz es singular si y solo si su determinante es nulo.

2.4 Transformaciones elementales por región. Escalonamiento de una matriz. Rango de una matriz.

Transformaciones elementales en las filas, Las fases de una matriz, Rango de una matriz

Si se intercambian dos filas cualesquiera de una matriz dada, llamamos a esta operación una operación de transformación elemental en las filas de una matriz. Se denota por R¬ij¬¬, lo cual implica que se intercambian las filas i y j de la matriz dada. Esta operación también se denota por R¬i¬ <→ R-j¬.

Un punto digno de notar es que esta operación no es de naturaleza singular. De hecho se ha demostrado, que todas las matrices no singulares son el resultado de la transformación elemental en la fila de una matriz . Si esto es cierto, entonces podemos concluir, que para todas las matrices no singulares también tenemos una matriz inversa, la cual tampoco es singular y es también el resultado de la transformación elemental en la fila de una matriz. Esta matriz elemental se denomina la matriz identidad I y tenemos el resultado A x I = A-1

En álgebra lineal, el rango de una matriz es el número máximo de columnas (filas respectivamente) que son linealmente independientes. El rango fila y el rango columna siempre son iguales: este número es llamado simplemente rango de A (prueba más abajo). Comúnmente se expresa como rg(A).

El número de columnas independientes de una matriz A de m filas y n columnas es igual a la dimensión del espacio columna de A. También la dimensión del espacio fila determina el rango. El rango de A será, por tanto, un número no negativo, menor o igual que el mínimo entre m y n:

2.3 Clasificación de las matrices.

Diferentes tipos de matriz

1). Matriz columna: Una matriz con n filas y 1 columna, se denomina matriz columna. Esta matriz es de tipo m x 1.

Por ejemplo: 

2). Matriz fila: Una matriz que tiene una fila y n columnas, se dice que es una matriz fila. Esta matriz es del tipo 1 x n.

Por ejemplo: 

3). Matriz Cuadrada: Una matriz en la cual el número de columnas es igual al número de filas, se conoce como una matriz cuadrada. Una matriz de orden n es aquella que tiene n filas y n columnas. La propiedad aceptada en la matriz cuadrada es que dos o más matrices cuadradas de orden idéntico, pueden multiplicarse, sumarse y restarse.

Por ejemplo: 

4). Matriz diagonal: En una matriz cuadrada, los elementos para los cuales i = j, se denominan elementos diagonales. Una matriz cuadrada donde cada elemento, excepto los elementos diagonales, son iguales a cero, es llamada matriz diagonal. La matriz diagonal se denomina a veces matriz diagonal rectangular.

Por ejemplo: 

5). Matriz identidad o unidad: Se dice que una matriz es la matriz identidad o unidad, si cada elemento de la diagonal principal de la matriz particular es 1. La matriz identidad generalmente es denotada por ‘I’. Este tipo de matriz tiene la siguiente propiedad:

AI = A y IA = A

Por ejemplo: 

6). Matriz cero o nula: Se trata de una matriz en la cual cada elemento es igual a 0. Se representa como ‘0’. Si ‘O’ es la matriz cero m × n y A es cualquier matriz m × n, entonces A + O = O A. En consecuencia O es la identidad aditiva de la suma de matrices.

Por ejemplo: 

7). Matriz simétrica: Una matriz simétrica se refiere a la matriz cuadrada cuyo valor es igual al transpuesto de la matriz. Es decir, .La simetría de la diagonal simétrica está relacionada con la diagonal principal. Por otra parte, toda matriz diagonal es simétrica.

Por ejemplo: 

8). Matriz asimétrica: La matriz asimétrica también es conocida como matriz antimétrica o antisimétrica. Se trata de una matriz cuyo valor de transposición es negativo de su valor. Es decir,

A = -AT.

-
Bibliografia:
 http://mitecnologico.com/igestion/Main/ClasificacionDeLasMatrices#sthash.vBxaEE8F.dpuf

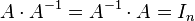2.2 Operaciones con matrices.

La matriz suma se obtienen sumando los elementos de las dos matrices que ocupan la misma misma posición; Para realizar la resta lo único que varia es el signo.

A continuación se muestran algunos ejemplos de operaciones que se realizan y la forma en que se resuelven las matrices.

2.1 Definición de matriz, notación y orden.

una matriz es una tabla cuadrada o rectangular de datos llamados elementos o entradas de la matriz, ordenados en filas y columnas.
Una matriz puede sumarse, multiplicarse y descomponerse varias formas. Comunmente se dice que una matriz m por n tiene un orden ("orden" tiene el significado de tamaño)

En la matriz una fila es cada linea horizontal y una columna es cada una de las lineas verticales.
Casi siempre, se denotan a las letras mayusculas mientras que se utilizan las correspondientes letras en minusculas para denotar a los elementos de las mismas.